THE DECIBEL.
Many of nature’s physical phenomena such as earthquakes, light and sound span a huge range of possible levels. Although an amazingly large portion of these ranges can be perceived by the human sensory systems, human perception has a strange property: it is often non-linear. It’s one of the reasons why, just as Richter did with earthquake strength, Alexander Graham Bell introduced a logarithmic representation of a physical phenomenon. In his case it was electrical audio transmission power over telephone lines, which we now know as the ‘Bel’. This ‘power quantity ratio’ representation sets a reference power level Po, and then relates the actual power under discussion to the reference as a decimal logarithmic ratio. The same concept can be applied to sound intensity - which is also a power quantity. The resulting parameter is actually a very useful representation of how humans perceive power and intensity:
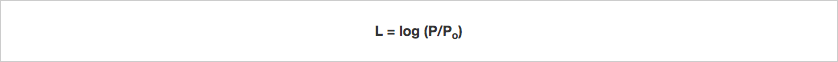
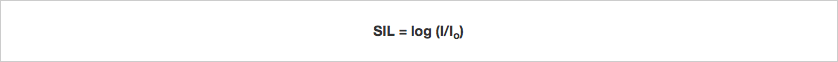
Where

Because of the logarithmic relationship of the Bel, multiplications can be carried out as simple additions, which is very convenient for fast calculations of power gain. However, when the professional audio world started to apply this concept in calculations, the ratio represented in ‘Bels’ turned out to be impractical, as in many cases the power ratios under discussion are below one Bell. For calculations there’s no problem at all, but in discussions the phrase ‘zero point something’ grows tiresome. Soon the term ‘decibel’ or dB was pitched, making discussing power ratios in human language more easy by applying a factor of 10 to the ratio:

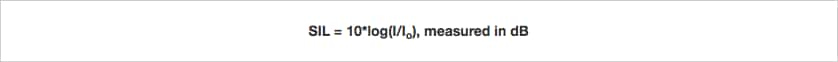
So far so good; double the power equals approximately 3dB and half power -3dB. These are nice round figures that can be pronounced even after a few beers. But after the introduction of logarithmic power quantity ratios, the professional audio world started to look primarily at field quantity ratios of voltages in electronics (Volt) and sound pressure in electro-acoustics (Pascal). These two field quantities are related to their respective power quantities as squares:


To keep consistency with the power ratio concept introduced by Bell, we started to represent voltage levels (G) and sound pressure levels (SPL) related to their associated power ratios, using the same dB scale we use for electrical power and sound intensity. However, to achieve a correct association between field quantity ratio and power quantity ratio, we have to apply the ratios of the squares of voltage (V) and sound pressure (p) to get the associated power quantity ratio in dB:


So, the ‘d’ in ‘dB’ in the G and SPL representations of voltage and sound pressure still refers to the factor 10 (‘deci’) used to make power comparison easy. But in the calculations, and in our interpretation and discussions, we use a factor of 20 to match the voltage and sound pressure levels to the associated power ratios in dB. The field factor is twice as high as the power factor, which sometimes has confusing consequences...
For example, a ‘factor of two’ increase in a voltage or sound pressure is represented by roughly 6dB, whereas a ‘factor of two’ increase of power or sound intensity is represented by roughly a factor of 3dB. Or, in other words; doubling a voltage or sound pressure value gives a 6dB higher output level, but it also requires 6dB more electrical power or sound intensity - which equals a factor of four, not two.
A practical case where this may lead to confusion is the calculation of the SPL output of a loudspeaker with a given amplifier power. The loudspeaker sensitivity is always given as ‘dBSPL@1W1m’: the SPL that will be generated at one metre distance on-axis if the loudspeaker is driven by a voltage that corresponds with one watt (in case of an 8Ω speaker that’s 2.84 volts). Let’s say that our loudspeaker has a sensitivity of 95dBSPL. If we drive it with 100W, we have to add the dB ratio of 100W to 1W. The trick is that, although we are calculating SPL - for which we normally use ‘20log’ to calculate ratios - in this case we have to add the power ratio, which uses ‘10log’. In our case this boils down to a 20dB power ratio, so the output SPL is 95dBSPL + 20dBP = 115dBSPL.
Of course if we had calculated the result using signal voltage levels, the result is exactly the same. To achieve a power amplifier output of 100W to 8Ω, we need to apply a voltage of 2.84 times the square root of 100, which calculates to 28.4V. The dB increase is then 20*log(28.4/2.84) = 20*1 = 20dB. But by using the power levels we can skip calculating the voltage levels, making engineering easier and quicker.
Although I have discussions and make electro-acoustic calculations every working day using decibels, I still have to keep reminding myself that dB at the end is about power ratios and that the ‘d’ represents a factor 10. If I think of a voltage ratio, the ratio in dB refers to the electrical power ratio that the voltage could generate if it was connected to a meaningful load (e.g. a dummy resistor). If I think of an SPL ratio, then the ratio in dB refers to the sound intensity ratio needed to produce the sound pressure ratio.






